隐马尔可夫模型最为成功的应用领域就是语言识别ASR和语音合成TTS。
这章内容,我想以语音识别作为一个切入点来讨论一下隐马模型,一方面可以总结一下之前做的工作,另一方面大家也可以了解一些语音相关的知识。
下面罗列一下本文的内容:
语音识别系统框架;
隐马尔可夫模型声学建模。
语音识别系统框架
首先贴一下语言识别的整个系统框架图,在这整个系统当中,声学模型是非常重要的核心模块,而这块的建模方法就是采用隐马模型进行建模,即为每个triphone建立各自的隐马模型。
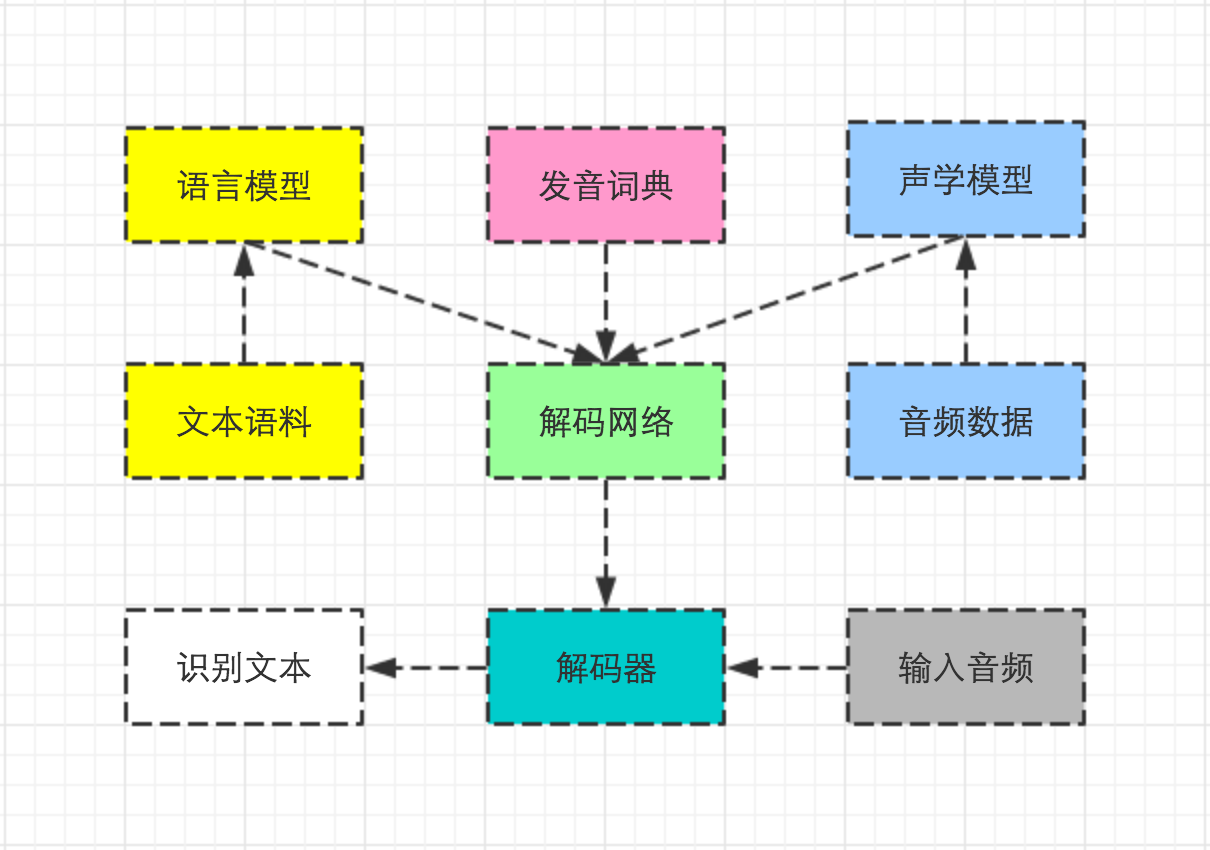
triphone是语音的最小建模单元,同时也意味着语音识别其实是从triphone这个粒度上开始的。
在深度学习出来之前,声学模型建模主要采用HMM+GMM,而现在主流都是采用HMM+DBN/LSTM进行建模。
这里先对triphone进行一个简单的介绍,实际当中的triphone可能不是这样,但基本是这个形式。
汉字: 语 音
拼音: yu yin
音子: y u y in
triphone: sil-y+u,y-u+y,u-y+in,y-in+sil
可以看出triphone实际上是含上下文的音素组合,因此它可以很好的模拟人说话协同发音的事实。
为什么采用对triphone进行建模,而不直接对词语进行建模呢?大致总结有以下几点原因:
词语体量大,而且随时间演化;
建模粒度粗,对发音细节刻画不够;
词粒度上建模,训练数据稀疏问题严重。
我们知道26个字母可以组成近75w的英文词汇,3500个常用汉字可以组成数不清个汉语词语,所以直接对词进行声学建模不是一个可取的方案。
如果在词这个粒度上进行建模,那么每个词的声学模型都会设计地很复杂且不统一,同时也很难捕捉词语发音的细节变化。因此,需要更细的粒度上进行建模,保证每个模型相对简单,而且更容易对发音进行统一建模。
另外,需要对每个词都进行音频采集从而获取足够的数据来对词语进行建模。但实际上,这个过程是非常耗时耗力的。如果选择对triphone建模,那么由于很多词都有着相同的发音单元,因此都可以用来对相应的triphone进行建模。
所以说,对triphone建模既可以很好地刻画发音的细节,又可以以不变应万变。因为不管词汇怎么变化,发音的基本组成单元是基本保持不变的,而且训练数据容易搜集。
以上,大致说明了一下语音识别系统中,声学建模的方法和建模单元的选择。
隐马尔可夫模型声学建模
这里,我们开始讨论怎么利用隐马模型进行triphone建模。还是先贴一张图吧。
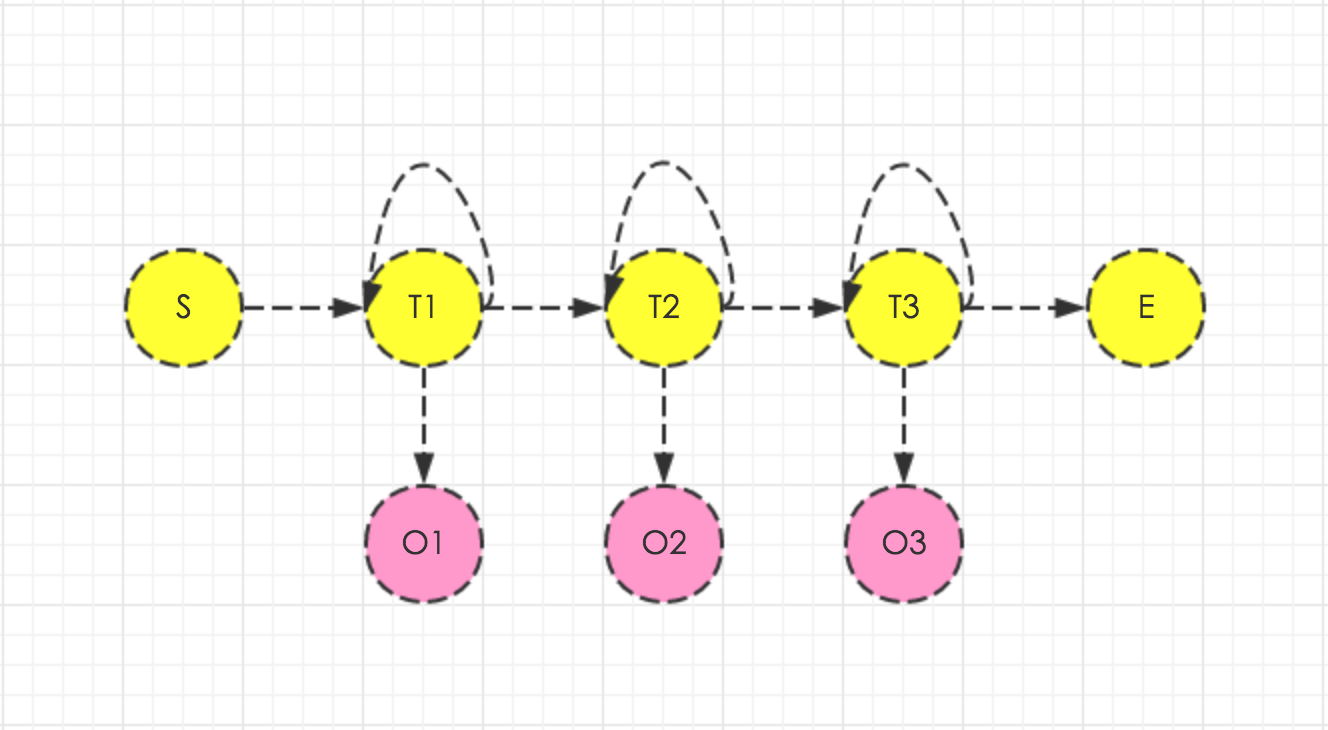
需要说明一下,图中黄色的圈圈代表triphone的5个状态(一般是5个,其中一头一尾是起始和结束状态),对应于隐马模型的内部状态。红色圈圈代表音频中提取的帧特征,对应着隐马模型的观测序列。
需要注意的是,triphone中的状态可以跳转到自己,因此可以模拟拖音和个体发音时长差异的现象。所以,triphone对应的隐马模型是非常有意思的,它的跳转是受限的,只能跳到自己或者下一个状态,而这些限制恰恰也是非常重要的。
另外,triphone隐马模型的内部状态其实对应的就是monophone。
好的,现在是时候详细讨论一下隐马模型了。
隐马模型
隐马模型包含内部状态、外部观测、以及各种概率。而所谓的隐马建模,本质上也是去估计状态之间的转移概率分布、状态的初始概率分布以及状态产生观测的条件概率分布,即隐马模型可以表示成\(λ=(A,B,π)\)。其中,\(A\)表示状态转移概率矩阵,\(B\)表示观测概率矩阵,\(π\)表示初始概率向量。
那么隐马模型的3个基本问题来了?
怎么计算生成特定观测序列的概率?
怎么根据观测数据,输出对应概率最大的内部状态序列呢?
怎么去计算这些模型参数呢?
对应到triphone建模这个问题上来看,一是怎么利用音频提取出来的帧特征估计对应隐马模型参数,二是选择出最有可能产生这些帧特征的隐马模型是哪个,这也就意味着音频帧序列对应的triphone序列被识别了出来。
如之前所说,隐马模型中,当前状态只依赖上一状态,而当前观测只依赖于当前状态,这就是齐次马尔可夫假设和观测独立性假设。
第一个问题
假设当前获取的帧序列为\(O=(o_1,o_2,o_3,…,o_T)\),某个triphone对应的隐马模型为\(λ=(A,B,π)\),问题等价于求\(P(O|λ)\)。
如果使用暴力破解法,可以直接使用全概率公式进行展开计算。
\[ P(O|λ) = \sum_I P(O|I,λ)P(I|λ)
\= \sum_{i_1,i_2,…,i_T} π_{i_1}b_{i_1}(o_1)a_{i_1i_2}b_{i_2}(o_2)…a_{i_{T-1}i_T}b_{i_T}(o_T) \]
但这种计算方式明显复杂度高,存在大量的冗余计算量。所以,隐马模型使用了动态规划算法,即前向后向算法。
前向算法
给定triphone对应的隐马模型\(λ=(A,B,π)\),记\(α_t(i)\)为到\(t\)时刻得到帧序列\(o_1,o_2,o_3,…,o_t\)且状态为\(s_i\)的概率为前向概率。
\[α_t(i) = P(o_1,o_2,o_3,…,o_t,i_t=s_i|λ)\]
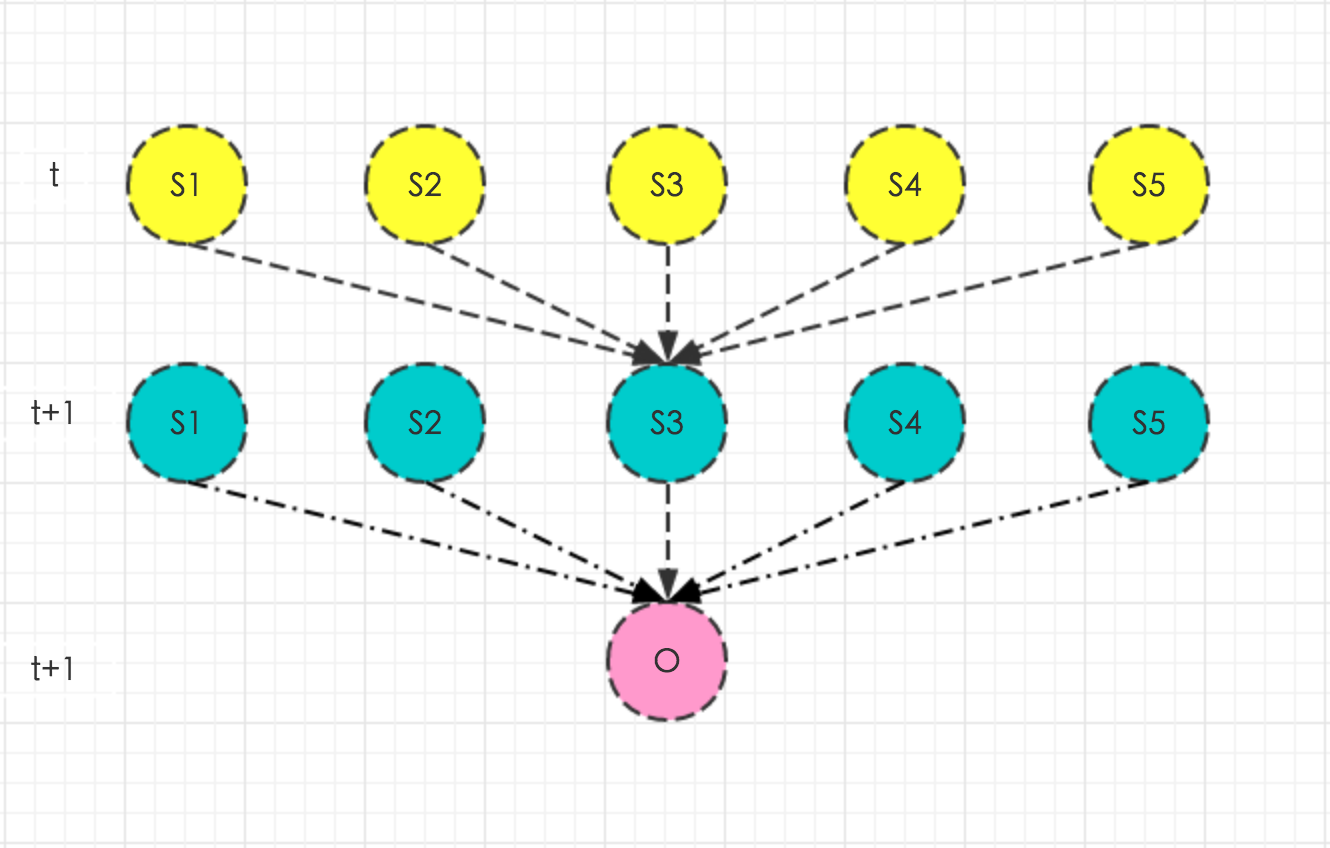
结合上图,很容易看出\(α_t(j)\)和\(α_{t+1}(i)\)之间的关系,即黄圈圈转移到绿圈圈并产生红圈圈的概率乘积和,黄圈圈代表前一时刻\(α_t(j)\)。
\[α_{1}(i) = π_ib_i(o_1) \]
\[α_{t+1}(i) = \sum_j α_{t}(j)a_{ji}b_i(o_{t+1})\]
\[P(O|λ) = \sum_j α_{T}(j) \]
所以,\(α_t(i)\)代表着\(t\)时刻观测到帧序列\(o_1,o_2,o_3,…,o_t\)且当前状态是\(s_i\)的概率。
因为当我们要算\(α_{t+1}(i)\)的时候,只需要保存上一时刻所有的\(α_{t}(j)\)就可以了,不需要保存再之前的前向概率,当然也不会出现重复计算的问题。
到这,第一个问题也就解决了。
后向算法
给定triphone对应的隐马模型\(λ=(A,B,π)\),记\(β_t(i)\)为到\(t\)时刻得到帧序列\(o_{t+1},o_{t+2},o_{t+3},…,o_T\)且状态为\(s_i\)的概率为后向概率。
\[β_t(i) = P(o_{t+1},o_{t+2},o_{t+3},…,o_T,i_t=s_i|λ)\]
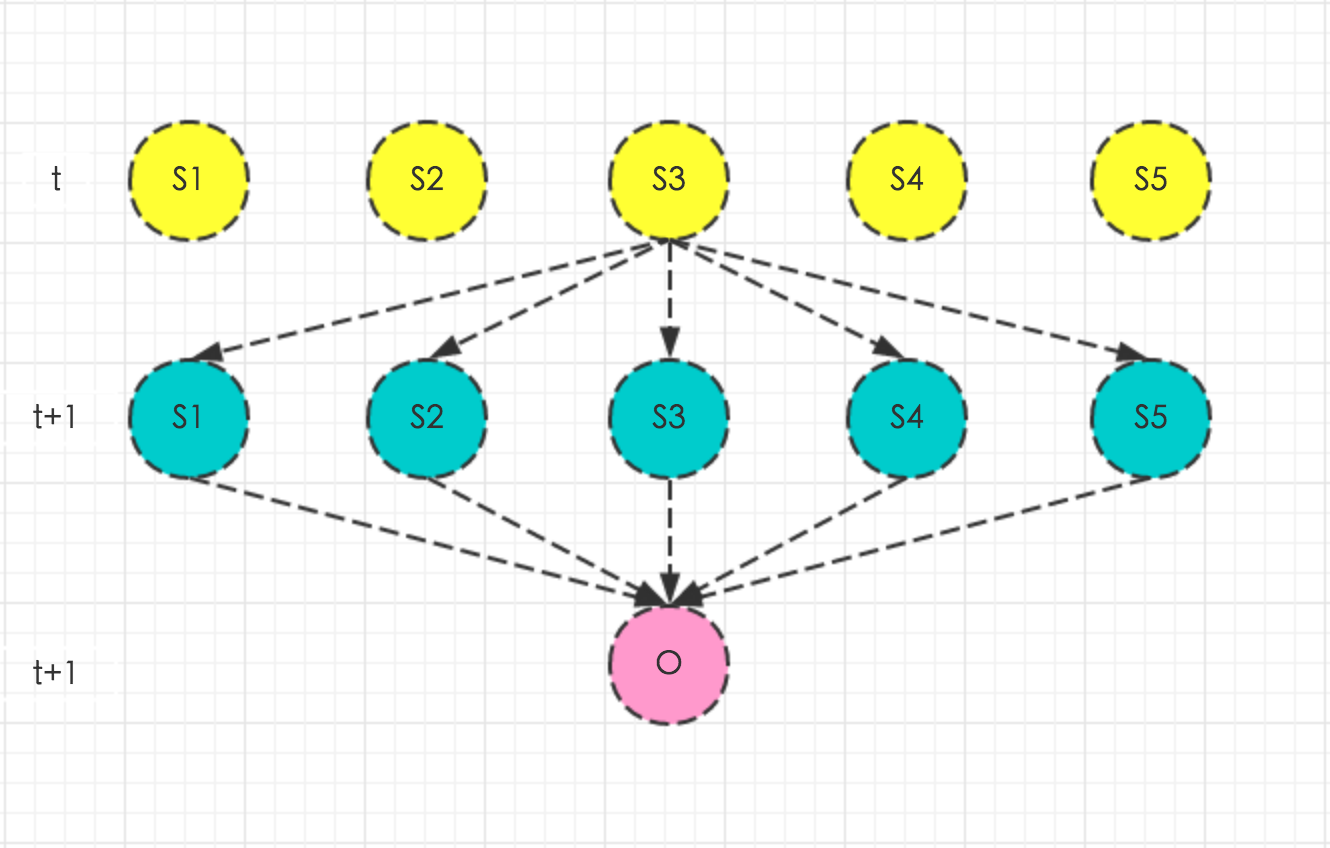
同样结合上图,很容易看出\(β_t(i)\)和\(β_{t+1}(j)\)之间的关系,即绿圈圈并产生红圈圈并由黄圈圈转移的概率乘积和,绿圈圈代表后一时刻\(β_{t+1}(j)\)。
\[β_{T}(i) = 1 \]
\[β_{t}(i) = \sum_j β_{t+1}(j)a_{ij}b_j(o_{t+1})\]
\[P(O|λ) = \sum_j β_{1}(j)π_jb_j(o_1) \]
所以,拥有和前向算法一样的优点,后向算法也可以算出特定帧序列出现的概率。
前向算法是求一个概率累积量的过程,而后向算法是求概率剩余量的过程。
结合前向算法和后向算法,可以得到:
\[P(O|λ) = \sum_i\sum_j α_{t}(i)a_{ij}b_j(o_{t+1})β_{t+1}(j) \]
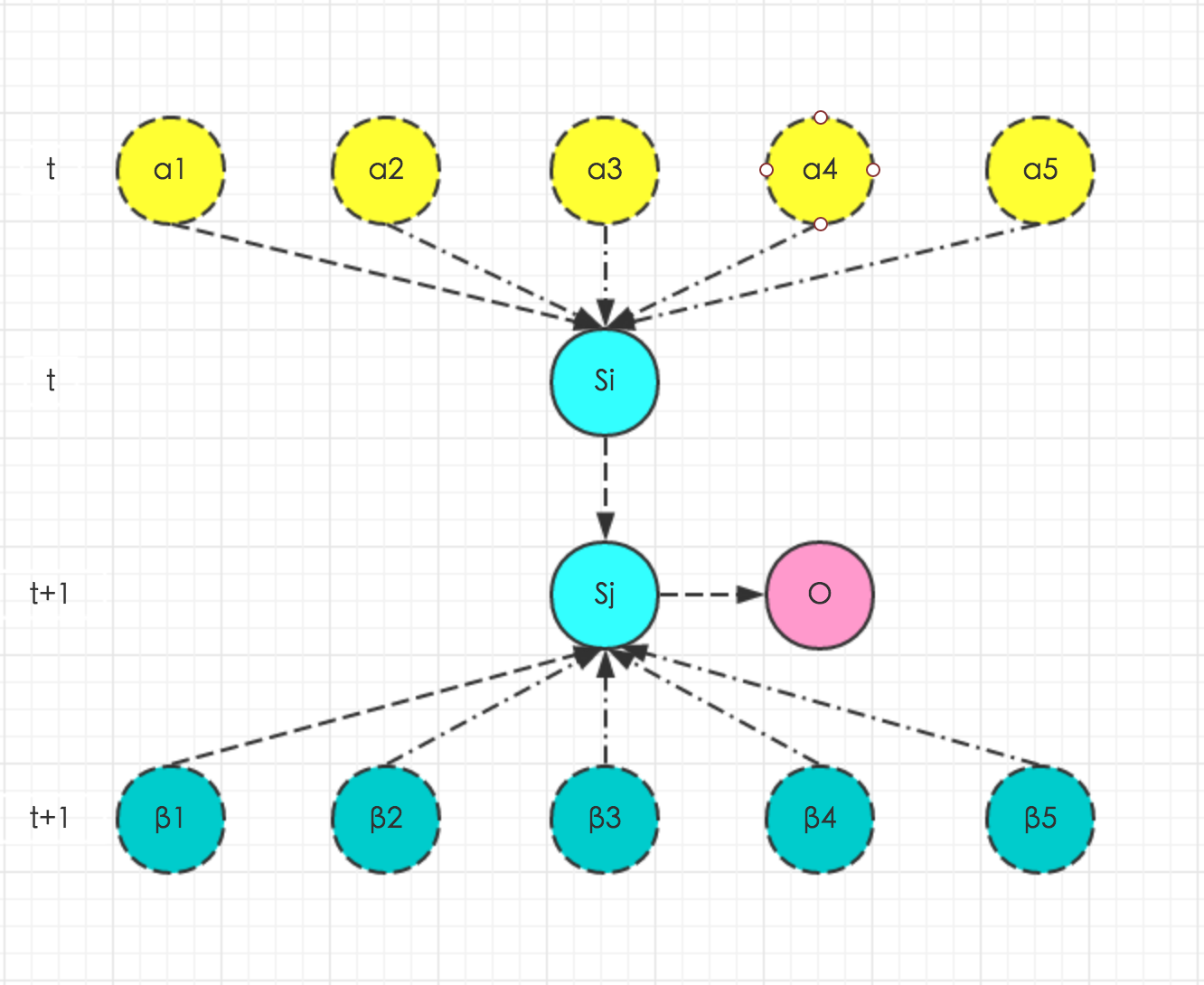
遍历\(t\)和\(t+1\)时刻所有的状态,结合前向和后向的概率进行帧序列出现概率的计算。
结合前向后向算法
为什么我们有了前向算法,还需要后向算法呢?这是因为结合两者可以导出一些概率的计算公式,而这些概率对于模型参数的估计有重要作用。
这些结论都是依据前向算法和后向算法的定义推导出来的。
- 给定模型\(λ=(A,B,π)\)和帧序列\(O\),在\(t\)时刻状态为\(s_i\)的概率。
\[P(i_t = s_i|λ,O) = \frac{α_{t}(i)β_{t}(i)}{\sum_j α_{t}(j)β_{t}(j)} \]
- 给定模型\(λ=(A,B,π)\)和帧序列\(O\),在\(t\)时刻状态为\(s_i\),\(t+1\)处于状态\(s_j\)的概率。
\[P(i_t = s_i,i_{t+1} = s_j|λ,O) = \frac{α_{t}(i)a_{ij}b_{t+1}(o_{t+1})β_{t+1}(j)}{\sum_i\sum_j α_{t}(i)a_{ij}b_{t+1}(o_{t+1})β_{t+1}(j)} \]
- 给定模型\(λ=(A,B,π)\)和帧序列\(O\),状态\(s_i\)出现的概率。
\[ \sum_{t=1}^TP_t(i_t = s_i|λ,O) \]
- 给定模型\(λ=(A,B,π)\)和帧序列\(O\),由状态\(s_i\)转移的概率。
\[ \sum_{t=1}^{T-1} P_t(i_t = s_i|λ,O) \]
- 给定模型\(λ=(A,B,π)\)和帧序列\(O\),由状态\(s_i\)转移到\(s_j\)的概率。
\[ \sum_{t=1}^{T-1} P_t(i_t = s_i,i_{t+1}=s_j|λ,O) \]
第二个问题
对于给定triphone对应的隐马模型\(λ=(A,B,π)\)以及帧序列为\(O=(o_1,o_2,o_3,…,o_T)\),要推算最有可能的内部状态序列帧序列\(S=(s_1,s_2,s_3,…,s_T)\)。
对于这个问题,有两种解决方法:近似方法和viterbi解码。
近似方法
\[s_t = argmax\ P_t(i_t = s_j|λ,O)\]
这样的求解并不能保证全局最优,只能作为参考。
Viterbi解码
Viterbi解码的思想类似于前向算法,只不过我们现在是要求概率最大的那条路径。
给定triphone对应的隐马模型\(λ=(A,B,π)\),记\(δ_t(i)\)为到\(t\)时刻得到帧序列\(o_1,o_2,o_3,…,o_t\)且状态为\(s_i\)的最优路径概率。
\[δ_{1}(i) = π_ib_i(o_1) \]
\[φ_1(i) = 0 \]
\[δ_{t+1}(i) = \max_{j} α_{t}(j)a_{ji}b_i(o_{t+1})\]
\[φ_{t+1}(i) = argmax\ α_{t}(j)a_{ji} \]
\[ \max_j δ_{T}(j) \]
\[ argmax\ δ_{T}(j) \]
和前向算法相比,就是把求和改成了求最大值,同时记录一下路径信息,即从上一时刻哪个状态转移到当前状态。
第三个问题
说了这么多,其实我们都是假设模型参数已知,那隐马模型的参数究竟怎样估计呢?现在我们开始讨论这个问题。
实际上,我们并不知道帧序列和内部状态的对应关系,所以无法直接用MLE极大似然估计法来估计模型参数。对于这种存在隐变量的参数估计问题,我们马上可以联想到EM算法。
之前提到,在深度学习之前,\(b(o_t)\)一般采用GMM混合高斯模型进行建模。
\[ p(x) = \sum_{j=1}^{K} ω_j N_k(x;μ_j,Σ_j)\]
EM算法分为两部走,第一步是求期望,即各种后验概率的计算;第二步是利用这些后验概率来更新当前模型参数。
E-Step
求不同时刻,各种状态的分布:\[γ_t(s_i) = P(i_t = s_i|λ,O)\]
求不同时刻,各种状态之间转换的分布:\[ξ_t(s_i
,s_j) = P(i_t = s_i,i_{t+1} = s_j|λ,O)\]
求帧到各状态混合高斯分布分量的后验分布:\[ρ_j(s_i,o_t) = P_{s_i}(j|o_t)\]
M-Step
更新各状态初始概率:\[ π_i^* = γ_1(s_i) \]
更新各状态之间的转移概率:\[ a_{ij}^* = \frac{\sum_{t=1}^{T-1}ξ_t(s_i
,s_j)}{\sum_{j=1}^N\sum_{t=1}^{T-1}ξ_t(s_i
,s_j)}\]
更新各状态各混合高斯分布分量的均值:\[ μ_j^* = \frac{\sum_{t=1}^Tρ_j(s_i,o_t)γ_t(s_i)o_t}{\sum_{t=1}^T γ_t(s_i)ρ_j(s_i,o_t)}\]
更新各状态各混合高斯分布分量的方差:\[ Σ_j^* = \frac{\sum_{t=1}^T ρ_j(s_i,o_t)γ_t(s_i)(o_t-μ_j)^T(o_t-μ_j)}{\sum_{t=1}^T γ_t(s_i)ρ_j(s_i,o_t)}\]
更新各状态混合高斯分布分量的权重:\[ ω_j^* = \frac{\sum_{t=1}^T ρ_j(s_i,o_t)γ_t(s_i)}{\sum_{j=1}^K\sum_{t=1}^T γ_t(s_i)ρ_j(s_i,o_t)}\]
总结
隐马模型涉及的知识还是很多的,我们主要需要了解隐马模型的两个独立性假设、前向后向算法、viterbi解码以及EM参数估计这些知识。
这里只是简单地从声学模型建模来切入讨论隐马模型的相关知识点,事实上声学模型建模过程远比这里说的复杂。
参考资料
统计学习方法 李航