隐马尔科夫模型可以看成朴素贝叶斯模型的链式扩展,而这里讨论的条件随机场模型可以看成最大熵模型的链式扩展。
和最大熵模型一样,条件随机场模型属于判别模型。和隐马模型相比,条件随机场不受限于隐马模型链式结构中过多的独立性假设,收益于最大熵模型借助特征函数可以纳入更多的上下文特征。
因此,在很多自然语言处理分类任务中,条件随机场的性能都可圈可点。比如,业界很多语义和分词方案是正则规则和CRF结果融合,而且这种方案在不少领域都满足了产品应用。
本节的内容包括:
条件随机场模型和最大熵模型
条件随机场模型和隐马模型
条件随机场模型和最大熵模型
一般条件随机场都特指线性条件随机场模型,即由最大熵模型线性扩展而来,可以更好地解决序列化标注的任务。
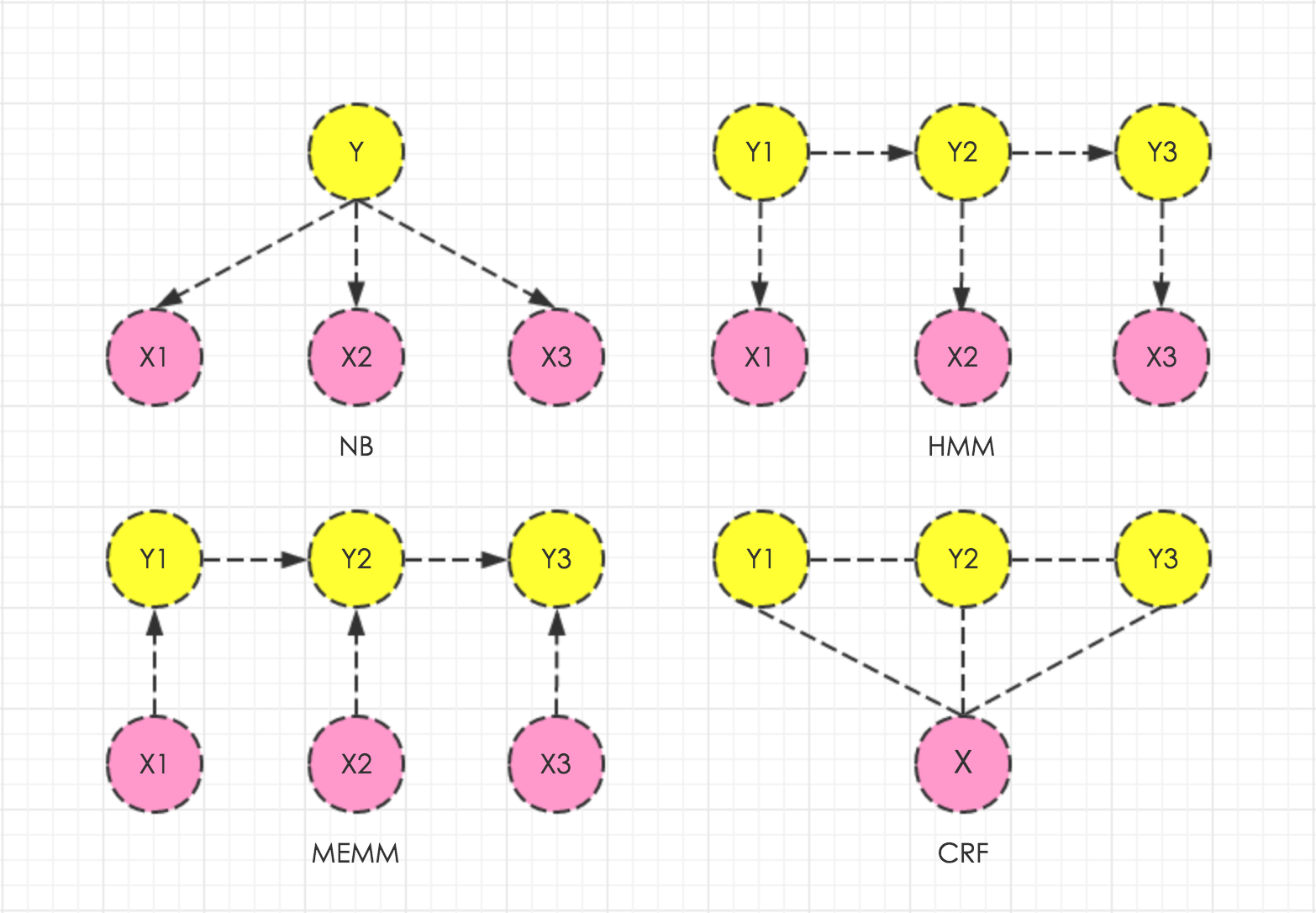
条件随机场模型和最大熵模型的关系,可以直接从两种模型的数学公式中了解一些。
最大熵数学模型:
\[ P_w(y|x) = \frac{exp(\sum_{j=1}^m w_jf_j(x,y))}{Z_w(x) } \]
\[ Z_w(x) = \sum_y exp(\sum_{j=1}^m w_jf_j(x,y)) \]
条件随机场模型:
\[ P_w(y|x) = \frac{∏_{i=1}^n exp(\sum_{j=1}^m w_jf_j(x,y_{i-1},y_i,i))}{Z_w(x) }
\ = \frac{∏_{i=1}^n exp(\sum_{j=1}^k w_jt_j(x,y_i,i)+\sum_{j=k+1}^m w_js_j(x,y_{i-1},y_i,i))}{Z_w(x)} \]
\[ Z_w(x) = \sum_y ∏_{i=1}^n exp(\sum_{j=1}^m w_jf_j(x,y_{i-1},y_i,i))
\ = \sum_y ∏_{i=1}^n exp(\sum_{j=1}^k w_jt_j(x,y_i,i)+\sum_{j=k+1}^m w_js_j(x,y_{i-1},y_i,i)) \]
可以看出来,条件随机场确实是最大熵模型在序列化任务上的一个扩展,特征函数不仅考虑了当前时刻的标注,而且也考虑了上一时刻的历史标注信息(借鉴隐马模型,但是是无向依赖)。另外,条件随机场可以利用滑动窗口引入更多的上下文观测信息,这可以对应于**CRF++**工具中的模版定义方法。
引入特征函数的目的以及意义之前在最大熵模型中已经讲过,这里不再细讲了。不过条件随机场模型所使用的特征函数包括两类:转移特征函数和状态特征函数。是不是类似隐马模型中的状态转移矩阵和观测概率矩阵?
条件随机场模型的推导就不详细展开了,因为结合其概率图以及最大熵模型特征函数知识可以很容易理解其模型公式。为了方便后续模型学习表示,这里需要给出条件随机场的矩阵公式:
\[ M_i(x) = [M_i(y_{i-1},y_i\ |\ x)] \]
\[ M_i(y_{i-1},y_i\ |\ x) = exp(W_i(y_{i-1},y_i\ |\ x))\]
\[ W_i(y_{i-1},y_i\ |\ x) = \sum_{j=1}^mw_jf_j(y_{i-1},y_i\ |\ x, i)\]
\[ P_w(y|x) = \frac{∏_{i=1}^{n+1} M_i(y_{i-1},y_i\ |\ x)}{Z_w(x) } \]
\[ Z_w(x) = ∏_{i=1}^{n+1} M_i(x)\]
\(M_i(x)\)为矩阵,其中每个元素代表当前样本\(x\)在\(i\)处出现\(y_i\)和\(y_{i-1}\)的概率。\(Z_w(x)\)可以理解为\(x\)对应所有可能标注路径的概率之和。
这里更倾向于表达条件随机场并不完全是全新的知识点,它是最大熵模型应用的延伸。这样的话,大家就会对概率图模型之间的关联关系有一定的认识,有助于我们更好地学习这些模型。
条件随机场模型和隐马模型
条件随机场除借鉴了隐马线性链式结构外,即相连状态构成最大团,另外包括前向后向算法以及维特比解码算法。
前向后向算法关系到条件随机场的模型学习,而维特比算法关系到条件随机场的模型预测。对比条件随机场和隐马模型的前向后向算法以及维特比算法,原理都是一致的,只不过各自概率因子计算方法不同。
和最大熵一样,条件随机场参数学习采用迭代尺度算法,具体的思路可以参考最大熵模型那节的内容。最终,我们得到的结论同样是:
\[ \sum_{x,y} P^-(x,y)f_i(x,y) = \sum_{x,y} P^-(x) P_w(y|x) f_i(x,y) exp(δ_i f^\#(x,y))\]
\[δ_i = \frac{1}{f^\#(x,y)}\frac{\sum_{x,y} P^-(x,y)f_i(x,y)}{\sum_{x,y} P^-(x) P_w(y|x) f_i(x,y)}
\ = \frac{1}{S}\frac{E_{P^{-}}(f_i)}{E_P(f_i)} \]
但需要注意的是,特征函数\(f_j(x,y)\)需要区分为\(t_j(x, y_i)\)和\(s_j(x,y_{i-1},y_i)\)。另外,概率\(P_w(y|x)\)的计算和最大熵不同,需要采用前向后向算法进行计算。
类似隐马模型,我们也需要定义前向和后向概率。
前向概率:
\[α_{0}(y=start|x) = 1 \]
\[α_{i}^T(y_i|x) = α_{i-1}^T(y_{i-1}|x)M_i(y_{i-1},y_i|x)\]
\[Z(x) = α_{n}^T(x) •1 \]
后向概率:
\[β_{n+1}(y=end|x) = 1 \]
\[β_{i}^T(y_i|x) = β_{i-1}^T(y_{i+1}|x)M_i(y_{i+1},y_i|x)\]
\[Z(x) = β_{1}^T(x) • 1 \]
这样,我们就可以用非常高的效率来计算\(P_w(y|x)\),并求解出\(δ_i\)。
通过定义前向和后向概率,用维特比算法求最优状态路径也就非常直观,所以这里就不再赘述了。
总的来说,条件随机场因为是对序列直接进行建模,因此需要借鉴隐马的动态规划算法进行参数估计。
##总结
一方面,条件随机场源自于最大熵模型,因此参数学习方法和最大熵模型一致,公式推导过程也可以参考学习;另一方面,条件随机场和隐马模型都是直接对观测序列建模,因此共用一些序列化任务求解的动态规划算法。
所涉及的知识点大多都是我们接触过,因此推荐参考这两个模型进行条件随机场的学习。
参考资料
Classical Probabilistic Models and Conditional Random Fields. Roman Klinger and Katrin Tomanek
统计学习方法 李航著